Kasiski Test - Part I
October 11, 2020
The tricky part of breaking the Vigenere cipher consists in finding the length of the key.
We discussed this in the breaking Vigenere post.
In that occasion we used the Hamming distance and the Index of Coincidence.
But another method existed much before the development of the IC around 1922.
In 1863, Kasiski published a method to guess the length of the secret key, method that we know today as the Kasiski test.
Let’s explore a \(O(\vert s \vert)\) solution with a worst case of \(O(\vert s \vert^2)\)
The naive solution
The Kasiski test consists in finding repeated ngrams in the ciphertext and measure the distance between them.
If there are repeated ngram in the plaintext that were leaked in the ciphertext, that means that the secret key was also repeated exactly in that part.
repeated ngrams
/----------/-----------/
ptext: 69 63 65 20 69 63 65 20 62 61 62 79
kstream: 73 6F 6E 67 73 6F 6E 67 73 6F 6E 67 (key = 73 6F 6E 67)
ctext: 1A 0C 0B 47 1A 0C 0B 47 11 0E 0C 1E
\----------\-----------\
repeated ngrams
It is perfectly possible to find repeated ngrams randomly, just by luck. Those are the “exceptions”.
I will talk about that in the second-part post.
With some exceptions, the distance between two repeated ngrams in the ciphertext must be then a multiple of the length of the key.
But for a particular ngram of length n, finding all the repeated ngrams requires scan the whole string, an effort of \(O(\vert s \vert)\), proportional to the size of the input string.
Repeating the process for all the ngrams of length n yields \(O(\vert s \vert^2)\).
And that’s only for n. Repeating everything again for the ngrams of length n+1, n+2 and so on blows up quickly to \(O(\vert s \vert^3)\).
No no, we can improve this.
The strategy
as_ngram_repeated_positions algorithm
We build the list of all repeated ngrams of length n using hashing in \(O(\vert s \vert)\) and not \(O(\vert s \vert^2)\).
merge_overlaping algorithm
This is an example of dynamic programming. Take a look of Automating the Cracking of Simple Ciphers, by Matthew C. Berntsen for a similar idea. code
Then, we build the list of the repeated ngrams of length n+1 reusing the finding of the previous step.
This will require \(O(g)\) where \(g\) is the size of the list built in the previous step.
While \(O(g) = O(\vert s \vert)\) in the worst case, it is expected to find very few repeated ngrams of length n so in the practice \(O(g) \ll O(\vert s \vert)\).
deltas_from_positions algorithm
The distances between the ngrams found can also be found in \(O(g)\).
The naive implementation would require \(O(g^2)\) but we can improve it a little.
frequency_of_deltas algorithm (aka the main)
frequency_of_deltas will combine all the previous algorithms.
It can be done roughly in \(O(\vert s \vert) + O(g^m)\) where \(m\) is the count of iterations that we repeat merge_overlaping.
In the worst case, \(O(g^m)\) behaves as \(O(\vert s \vert^2)\) and frequency_of_deltas will be quadratic.
But as we said, we don’t expect to find many repeated ngrams so the term \(O(g^m)\) will be negligible and frequency_of_deltas will remain linear.
We have the strategy, now we need the correct tools.
Data structures
We will use the following data structures:
- dictionaries: with \(O(1)\) for insertion or update of a key.
- lists: with \(O(1)\) for append and \(O(n)\) for iteration.
- default-dictionaries: like the dictionaries but with the handy shortcut to create and add an entry in the dictionary if the key requested is not present.
Python is not the fastest language but it has all the tools needed.
Let’s start!
Repeating ngram list - as_ngram_repeated_positions algorithm
We are interested in to find all the positions of every single repeated ngram in the text.
Focus only on the ngrams of 2 characters for now.
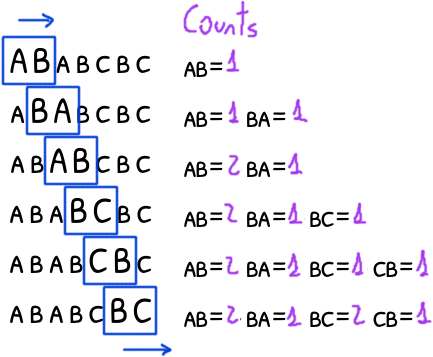
We need to count how many instances of the same ngram are, so we can know which are unique; and we need to track their position, so we can later know the distance between them.
Storing every ngram instance in memory is expensive (for a 2 characters ngram you will have to store twice the source string).
A simple solution is to use an id: different ngrams will have different ids while the instances of the same ngram will have the same id.
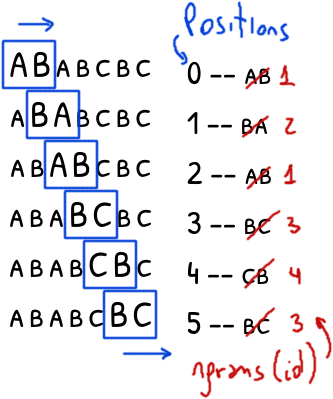
The following Python fragment summarizes the above:
# input: s, the original text
id_of_ngram = {0:0}
pos_sorted = []
ngram_cnt_by_id = defaultdict(int)
ngram_cnt_by_id[0] = 0 # id==0 is reserved for deletions, see later
for pos, ngram in enumerate(s.ngrams(2)):
id = id_of_ngram.setdefault(ngram, len(id_of_ngram))
pos_sorted.append((pos, id))
ngram_cnt_by_id[id] += 1
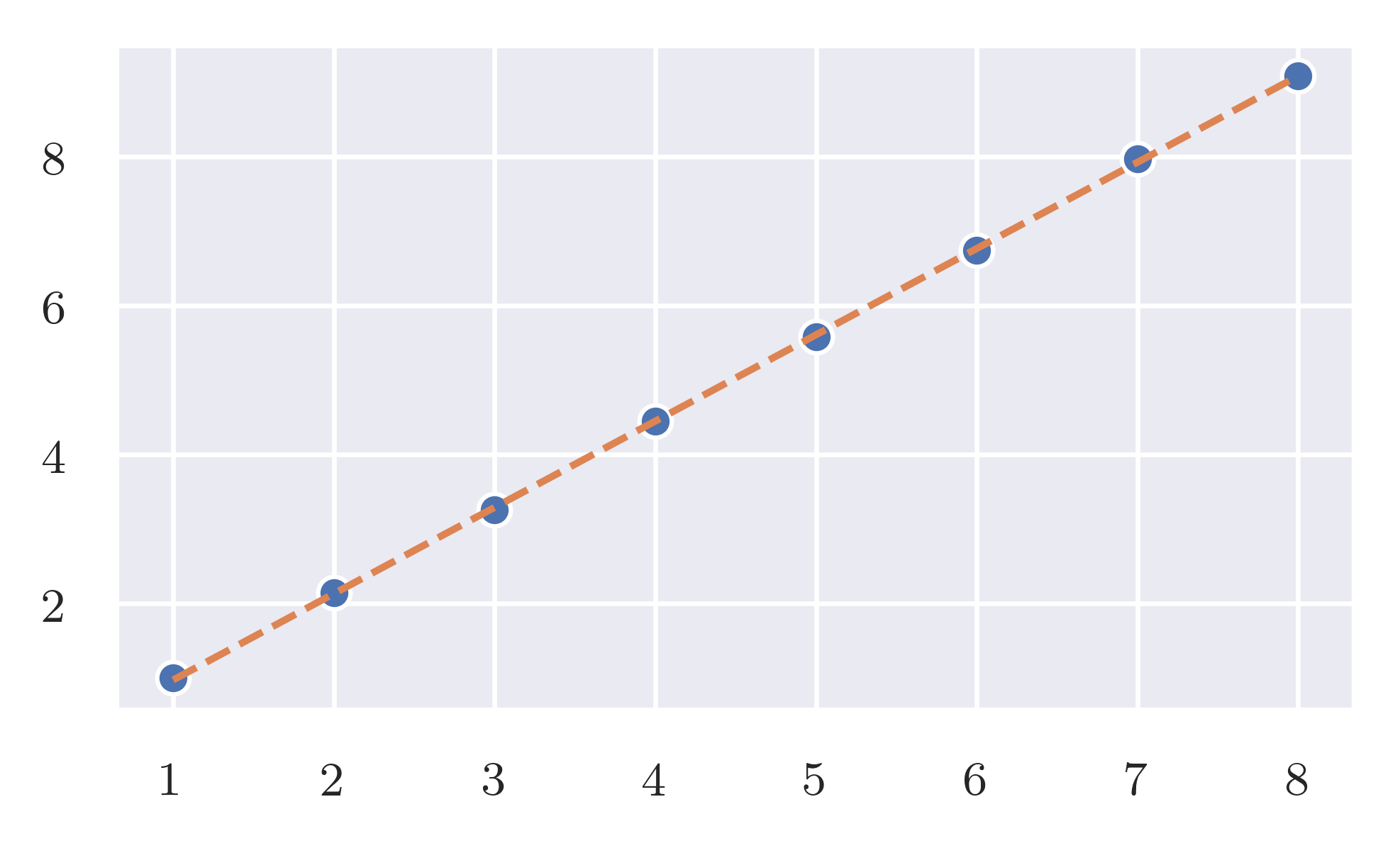Input-size/time-taken relationship of as_ngram_repeated_positions. code
For a string of \(\vert s \vert\) characters the algorithm generates a list of \(\vert s \vert\) tuples. If chosen the data structures correctly, the algorithm runs in \(O(\vert s \vert)\) (linear time and space).
One final step remains: once we have the list we need to filter out any unique ngram (those that have a counter of less than 2).
This is also linear.
pos_sorted = [(p, id) for p, id in pos_sorted
if ngram_cnt_by_id[id] > 1]
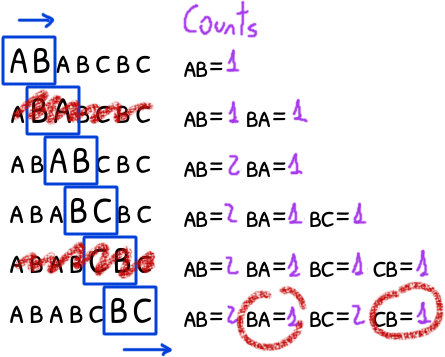
The final result is a list of tuples (position, id) with the positions of the ngrams and their identifiers sorted by their position.
The algorithm can be generalized to find all the non-unique ngrams of length n changing s.ngrams(2) to s.ngrams(n).
The trick is how to build the list of ngrams of n+1 length reusing the ngrams of length n found by the above algorithm.
Superior ngram order - merge_overlaping algorithm
The idea is that two ngrams g_1 and g_2 of n characters at positions p_1 and p_2 in the original string can be merged and build a ngram of n+1 bytes at p_1 if and only if p_1 + 1 == p_2.
In other words, they are consecutive.
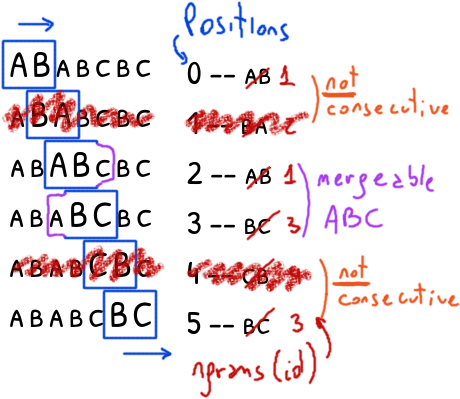
A merged ngram not necessary means that it is a repeated ngram but we know that any repeated ngram will be a merged one.
id_of_ngram = {0:0}
ngram_cnt_by_id = defaultdict(int)
ngram_cnt_by_id[0] = 0
for ix, (cur, nex) in enumerate(zip(pos_sorted[:-1], pos_sorted[1:])):
pcur, id = cur
pnex, id2 = nex
if pcur + 1 != pnex:
pos_sorted[ix] = (0, 0) # delete later (index 0 is special)
else:
# the id of the merged ngram is formed by the ids of the
# original pair of ngrams.
id = id_of_ngram.setdefault((id, id2), len(id_of_ngram))
pos_sorted[ix] = (pcur, id) # new ngram
ngram_cnt_by_id[id] += 1
# the last position P1 always is "deleted" because there is
# not P2 such P1 + 1 == P2 *and* P1 < P2 (basically because there
# are no more positions after P1)
pos_sorted[-1] = (0, 0)
During the scan we also count how many ngrams we built: unique ngrams are filtered later in linear time removing the false positives.
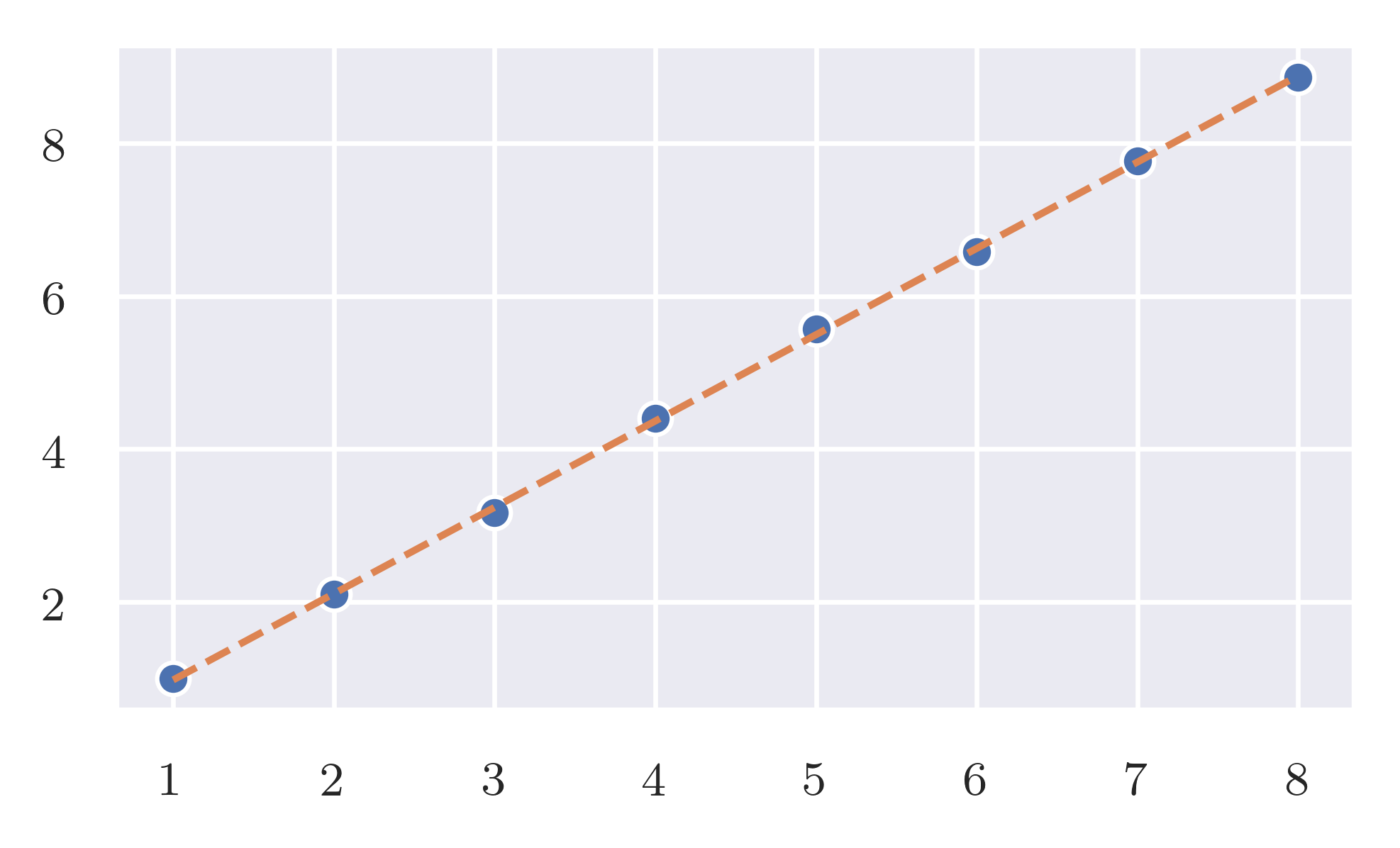Input-size/time-taken relationship of merge_overlaping. code
pos_sorted = [(p, id) for p, id in pos_sorted
if ngram_cnt_by_id[id] > 1]
merge_overlaping is a linear operation in terms of the initial pos_sorted list not in terms of the length of the input strings.
In the practice this means that merge_overlaping – \(O(g)\) – will be faster than as_ngram_repeated_positions – \(O(\vert s \vert)\).
Computing the gaps - deltas_from_positions algorithm
Now that we have the position of each repeated ngram we want to calculate the distance between them.
We are interested in the distance between the same ngrams.
This is because we assume that the same repeated ngram in a ciphertext is due the encryption of the same plaintext and the repeating key of Vigenere was aligned.
The distance should be then a multiple of the length of the key.
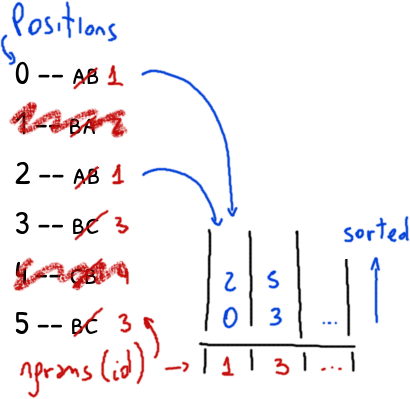
# group first
pos_grouped = defaultdict(list)
for pos, id in pos_sorted:
pos_grouped[id].append(pos)
# compute the gaps later
delta_stats = Counter()
for positions in pos_grouped.values():
d = (y-x for x, y in zip(positions[:-1], positions[1:]))
delta_stats.update(Counter(d))
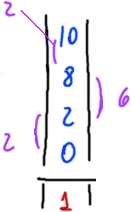
We simplify the maths and calculate then the difference between consecutive positions for a given ngram.
We assume that difference between non-consecutive values will yield a multiple of the previous shorter difference hence it will be also a multiple of the key length.
In other words, calculating the “multiple of the multiple” does not add any new information.
Frequency of deltas - frequency_of_deltas algorithm
Basically we put all the algorithms to work together:
res = []
pos_sorted = as_ngram_repeated_positions(s)
while pos_sorted:
delta_stats = deltas_from_positions(pos_sorted)
res.append(delta_stats)
pos_sorted = merge_overlaping(pos_sorted)
Here are some examples using cryptonita
>>> from cryptonita import B
>>> from cryptonita.stats.kasiski import frequency_of_deltas
>>> s = B(b'ABCDBCDABCDBC')
>>> frequency_of_deltas(s)
[Counter({7: 3, 3: 1, 4: 1}), Counter({7: 3}), Counter({7: 2}), Counter({7: 1})]
>>> s = B('1A0C0B471A0C0B47110E0C1E', encoding=16)
>>> frequency_of_deltas(s)
[Counter({4: 2}), Counter({4: 1})]
In the last example the first Counter is for the ngrams 1A 0C 0B and 0C 0B 47 where found repeated at a distance of 4 once each one (2 in total). The second Counter is for 1A 0C 0B 47 repeated once at a distance of 4.
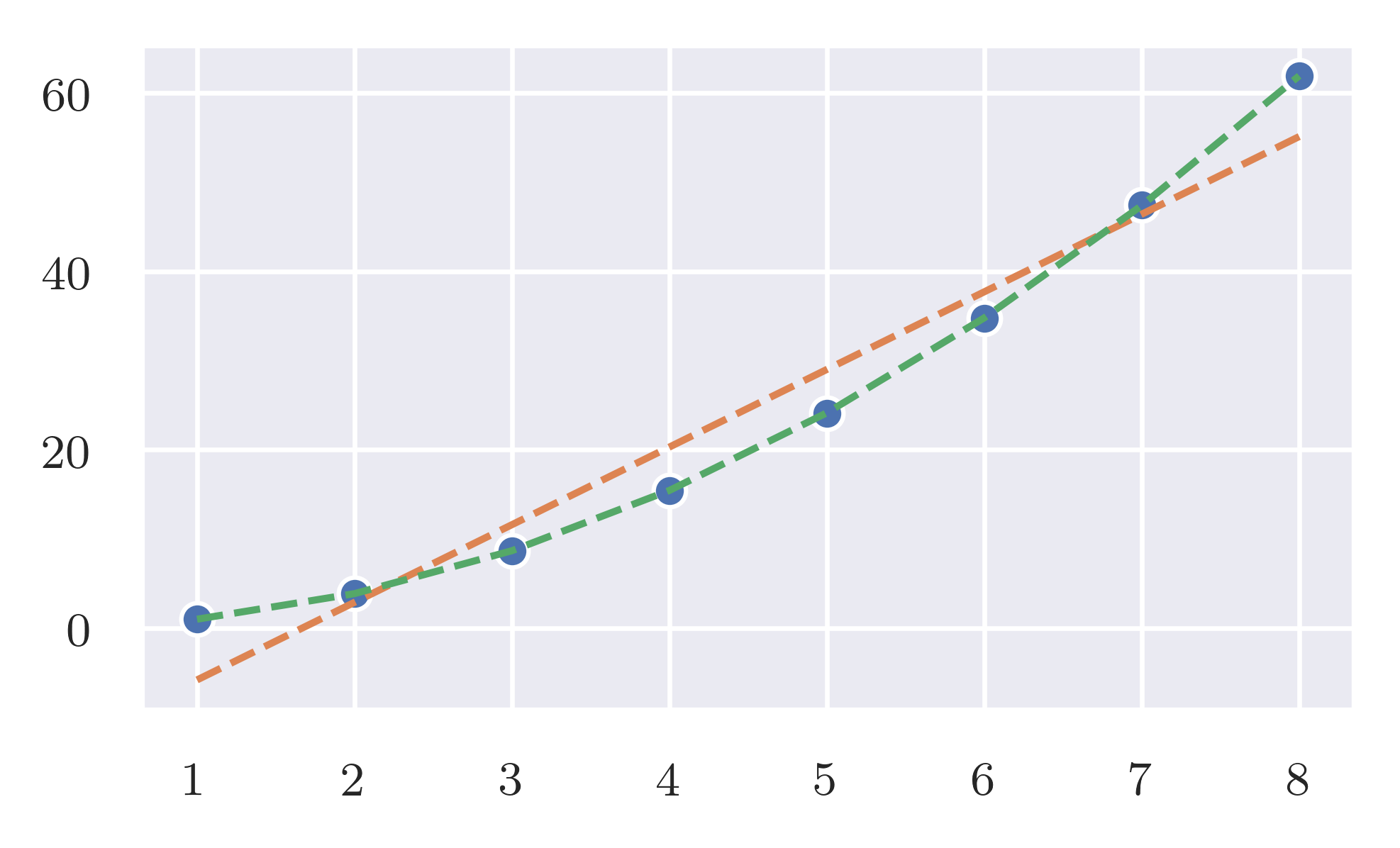
As predicted the expected effort is linear while the worst case is quadratic.
Expected case. frequency_of_deltas has a linear response when the size of the input increase linearly. code
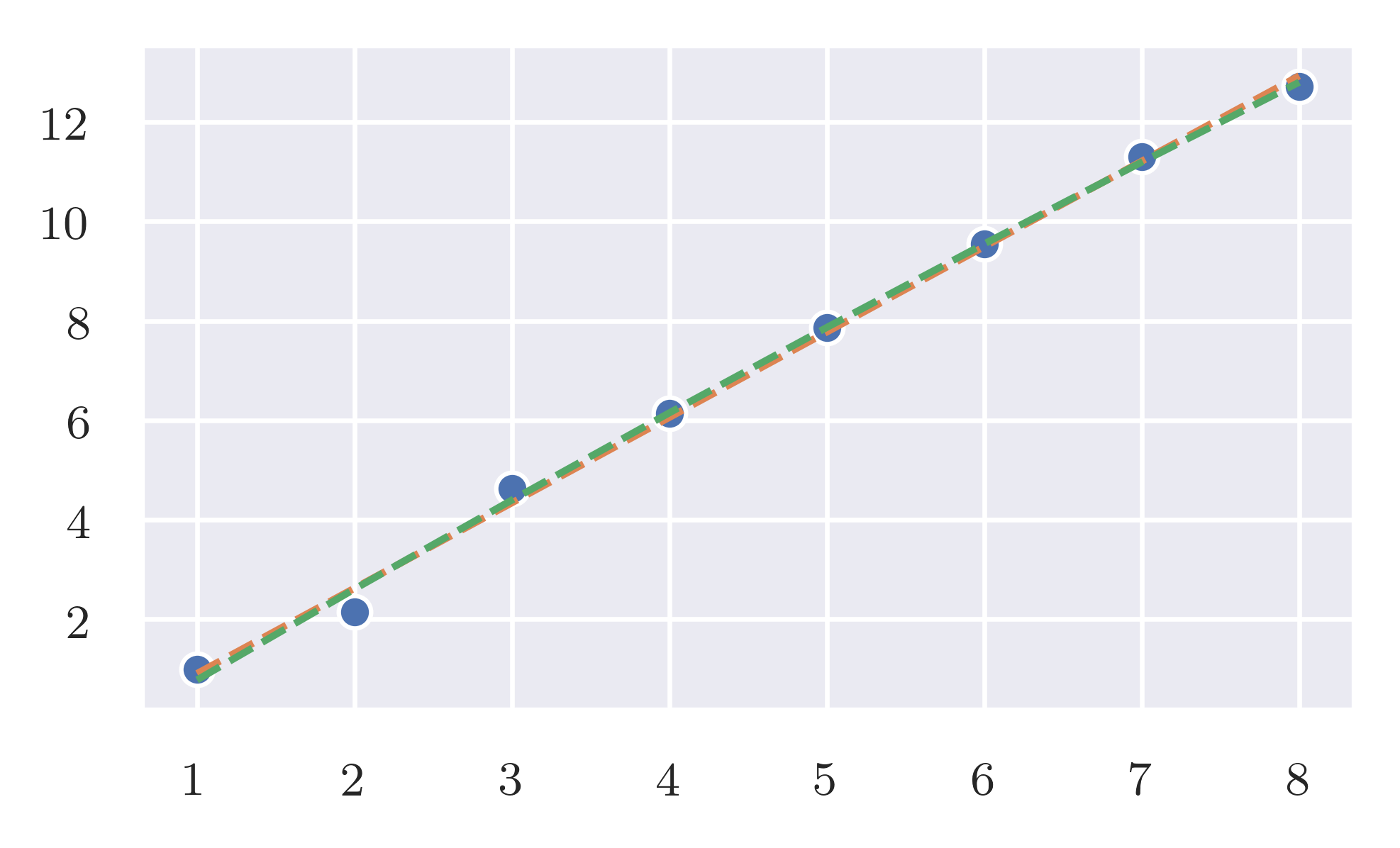
Worst case. frequency_of_deltas has a quadratic response when the size of the input increase linearly. Even with this result, it is better than cubic the naive implementation. code
Final thoughts
With frequency_of_deltas we have the most likely difference or gap, gap that it should be a multiple of the length of the key.
But what if a repeated ngram happen just by luck?
That’s for the Part II.