Index of Coincidence Explained
October 4, 2019
The concept of Index of Coincidence was introduced by William Friedman in 1922-1923 in the paper titled “The Index of Coincidence and its Applications in Cryptoanalysis” [1].
The Navy Department (US) worked in the following years on this topic coming, in 1955, with a paper titled “The Index of Coincidence” by Howard Campaigne [2].
However I found some confusing and misleading concepts in the modern literature.
This post is a summary of what I could understand from Howard’s work.
Count Coincidences
How similar are two strings?
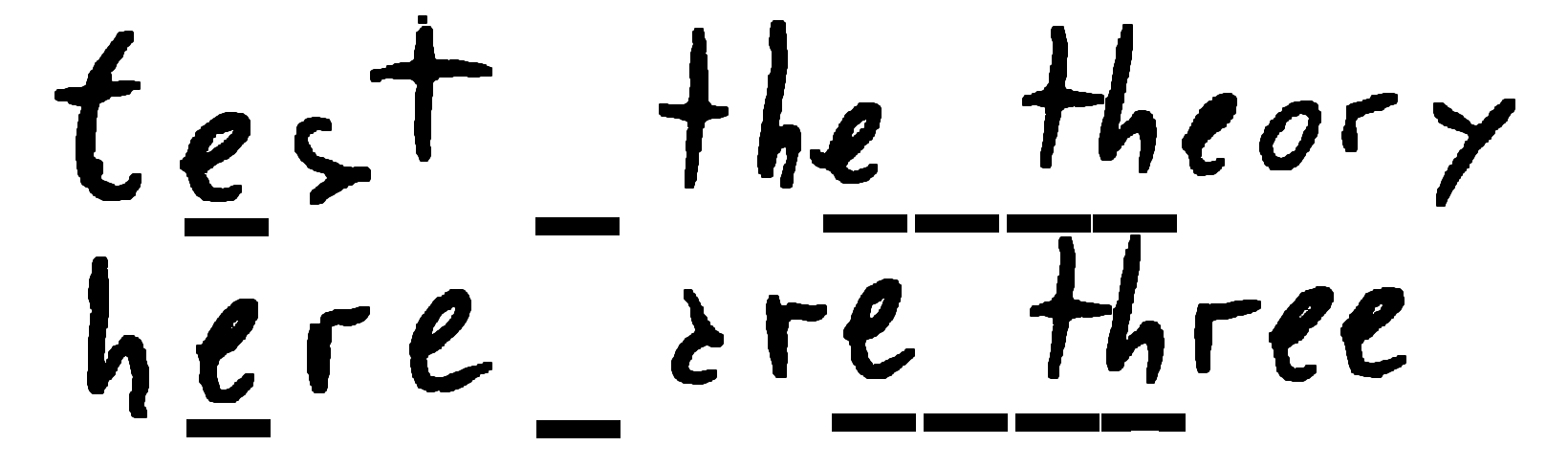Two strings aligned have 6 coincidences.
Put the two strings one below the other, perfectly aligned. Now, column by column, count how many times the same letter appear in the same column.
Two strings that have substrings in common and aligned have a lot of coincidences.
We will call this Aligned Count of Coincidences or \(AC(s_1,s_2)\).
Two strings, the second shifted 4 positions to the right, have 3 coincidences.
But if the substrings are not aligned we may think, incorrectly, that two strings does not have nothing in common.
Two strings, the second shifted 6 positions to the left, have 3 coincidences too.
So we define the Count of Coincidences \(C(s_1,s_2)\) between two strings as how many columns have the same letter for every possible alignment.
It’s more simple than it looks.
Count for Every Possible Alignment
Pick the first e of the first string. It will have a coincidence with every possible e in the second string.
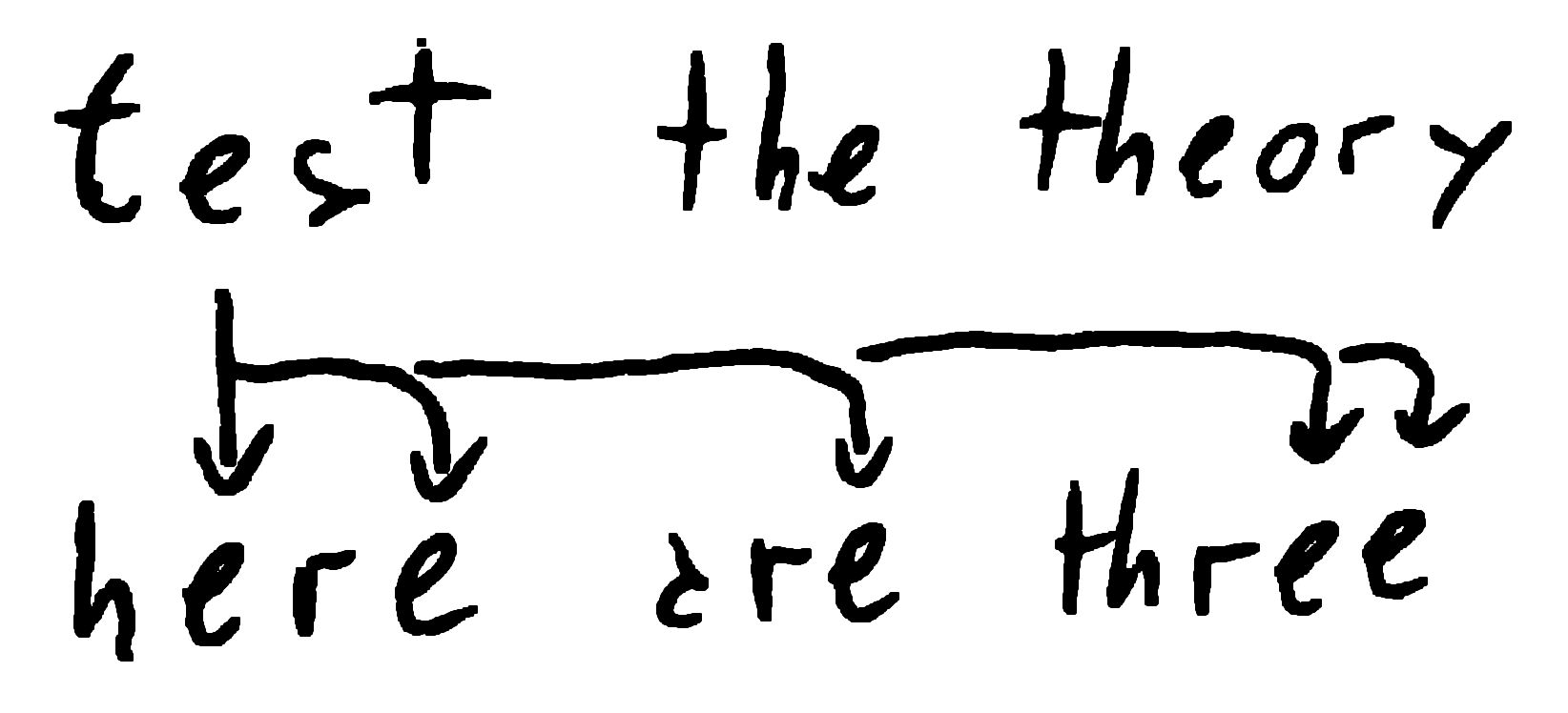Coincidences of the first e with all the e of the second string.
There are 5 letters e in the second string, so we will have 5 coincidences.
Then pick the second e of the first string and repeat. Another 5 coincidences.
The first string has 3 letters e so at the end we will have 3 times 5, 15 coincidences.
In general for a particular byte we will have \(n_i m_i\) coincidences where \(n_i\) is the count of that byte in the first plaintext and \(m_i\) in the second.
For all the possible bytes \(i\), the count of coincidences for all the possible shifts and alignments is:
$$ C(s_1,s_2) = \sum_{\forall i} n_i m_i \tag{1}\label{Coincs1s2}$$Expected Count
The equation \((\ref{Coincs1s2})\) counts the coincidence between two particular instances.
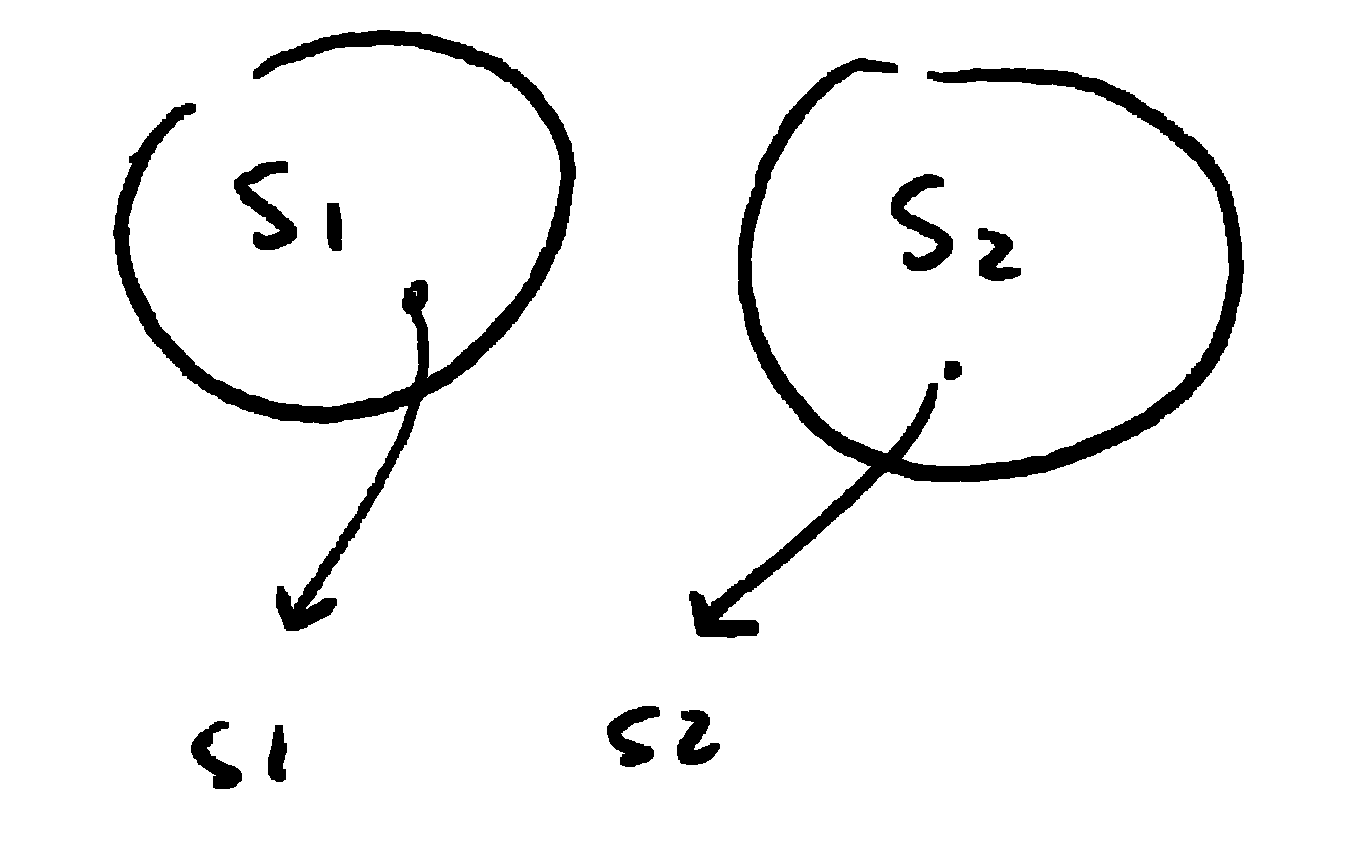Two sets or families of strings \(S_1\) and \(S_2\); \(s_1\) and \(s_2\) are just two examples of those.
Instead of comparing two particular strings we compare two families of strings where the probability of each symbol \(i\) is \(p_i\) in the first family and \(q_i\) in the second.
Because \(p_i\) and \(q_i\) are independent, the probability of picking the same letter or symbol \(i\) is \(p_i q_i\).
Picking one letter or other are mutually exclusive events (disjoin events) so the probability of having any coincidence is the sum:
$$ PrC(S_1,S_2) = \sum_{\forall i} p_i q_i \tag{3}\label{PrCoincS1S2}$$The equation \((\ref{PrCoincS1S2})\) is shown in [Howard], equation (25)
With \((\ref{PrCoincS1S2})\), the expected count for two strings of length \(N\) taken from the families \(S_1\) and \(S_2\) is:
$$ EC(S_1,S_2) = N \sum_{\forall i} p_i q_i \tag{4}\label{ExpCoincS1S2}$$[Howard], equation (pseudo 2.5)
Expected Coincidences Between Two Random Strings
If we are comparing two uniformly distributed random strings, all the letters or symbols have the same probability so \(p_i = q_i = \frac{1}{c}\) where \(c\) is the length of the alphabet (256 for bytes, 26 for English letters, …)
$$ \begin{align*} PrC(R) & = \sum_{\forall i} p_i q_i \tag{3}\\ & = \sum_{\forall i} \frac{1}{c} \frac{1}{c} \\ & = c \frac{1}{c} \frac{1}{c} \\ & = \frac{1}{c} \tag{5}\label{PrCoincR} \end{align*} $$And therefore the expected count is
$$ EC(R) = N \sum_{\forall i} p_i q_i = \frac{N}{c} \tag{6}\label{ExpCoincR}$$Cross Index of Coincidence
Finally, we define the Cross Index of Coincidence, \(IC(s_1,s_2)\) for short, as the ratio between the count of coincidences between two strings (\(s_1\) and \(s_2\)) of the same length \(N\) and the expected coincidences assuming uniformly distributed random strings.
In other words is the ratio between equations \((\ref{Coincs1s2})\) and \((\ref{ExpCoincR})\)
$$ IC(s_1,s_2) = \frac{C(s_1,s_2)}{EC(R)} = \frac{c}{N} \sum_{\forall i} n_i m_i \tag{7}\label{IdxCoincs1s2}$$We can also use \(AC(s_1,s_2)\) instead of \(C(s_1,s_2)\) and we will get another variant of \(IC(s_1,s_2)\).
\(c\) is Not a Normalization Factor
I found in modern literature than the term \(c\) is explained as a normalization factor. Far from being truth.
In fact, the values that \(IC(s_1,s_2)\) go from 0 to \(cN\).
A normalized IC can be obtained from \((\ref{IdxCoincs1s2})\) if we divide it by \(cN\) that it is the same to ask for \(PrC(S_1,S_2)\):
$$ \begin{align*} IC_N(s_1,s_2) & = \frac{c}{N} \sum_{\forall i} n_i m_i \frac{1}{cN} \\ & = \frac{c}{c} \sum_{\forall i} \frac{n_i}{N} \frac{m_i}{N} \\ & = \sum_{\forall i} p_i q_i \\ & = PrC(S_1,S_2) \tag{3} \end{align*} $$Cross Index of Coincidence between Two Families
If we calculate the ratio between \((\ref{PrCoincS1S2})\) and \((\ref{PrCoincR})\) we have a way to compare families without needing the length:
$$ IC(S_1,S_2) = c \sum_{\forall i} p_i q_i \tag{9}\label{IdxCoincS}$$Auto Index of Coincidences
There is another definition of IC that compares a string with itself.
It follows a similar counting process: put the string and its copy in two rows, count the coincidences, shift one place and repeat.
Of course there is a case where both will have a full match. That case is ignored.
The count of auto coincidences is:
$$ C(s) = \sum_{\forall i} n_i (n_i-1) \tag{10}\label{Coincs} $$In term of the probabilities:
$$ PrC(S) = \sum_{\forall i} p_i (p_i-1) \tag{11}\label{PrCoincS}$$Once again, the IC is a ratio between the actual coincidences \(C(s)\) and the expected coincidences \(\frac{N}{c}\):
$$ IC(s) = \frac{c}{N} \sum_{\forall i} n_i (n_i-1) \tag{12}\label{IdxCoincs}$$Or it is the ratio between the probabilities:
$$ IC(S) = c \sum_{\forall i} p_i (p_i - 1) \tag{13}\label{IdxCoincNormS}$$Final Thoughts
This post took me a lot of time. The topic is not complex and the maths are very simple but it is the amount of several and slightly different definitions that makes hard to read and interpret.
Counting the coincidences between two strings aligned \(AC(s_1,s_2)\), not aligned \(C(s_1,s_2)\), the probability of having a coincidence \(PrC(S_1,S_2)\), the expected count, the \(IC\), …
I hope to got it right in this post :D
Related tags: cryptography, index of coincidence