Detecting Penguins

May 20, 2018

The ECB encrypted image on the right and its plaintext original version on the left. Image taken from wikipedia.

⊕ – Spoiler Alert! –

Can you see the penguin?

Warming up

The following ciphertext was encrypted with AES in Electronic Codebook mode (ECB) with the given key.

In ECB each plaintext block is encrypted using the same key.

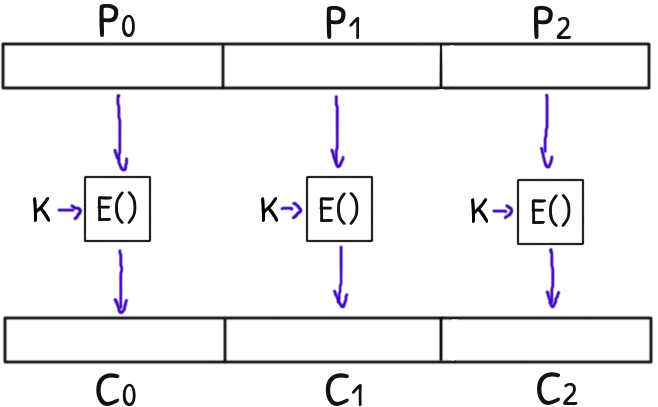
Decrypting is a piece of cake; this is just to get practice about AES in ECB mode

>>> from cryptonita import B, load_bytes     # byexample: +timeout=10

>>> ciphertext = B(open('./posts/matasano/assets/7.txt'), encoding=64)
>>> blocks = ciphertext.nblocks(16)

>>> key = B('YELLOW SUBMARINE')

>>> from Crypto.Cipher import AES
>>> plaintext = B.join(AES.new(key, AES.MODE_ECB).decrypt(b) for b in blocks)

>>> print(plaintext)
b"I'm back and I'm ringin' the bell<...>Play that funky music \n\x04\x04\x04\x04"

Note how to encryption/decryption of one block don’t depend of any other: this allows the encryption/decryption to be at random places and in parallel.

Detecting Penguins

If two plaintext blocks are the same, ECB will encrypt them to the same ciphertext block.

Detecting AES in ECB mode from a pool of random strings is therefore trivial: if the plaintext has two or more equal blocks, the ciphertext will have the same blocks repeated, something unlikely for a truly random string.

We can use the same technique done in the previous post for detecting coincidences.

>>> ciphertexts = list(load_bytes('./posts/matasano/assets/8.txt', encoding=16))

>>> from cryptonita.metrics import icoincidences
>>> scores = [icoincidences(c) for c in ciphertexts]

>>> scores_and_indexes = [(s, i) for i, s in enumerate(scores)]
>>> scores_and_indexes.sort()
>>> scores_and_indexes[-3:] # higher values, less random
[(0.00526729<...>, 92),
 (0.00526729<...>, 173),
 (0.01305031<...>, 132)]

>>> methods = {}
>>> methods['IC - Byte sequence'] = scores

Instead of working at the byte level, we can work with blocks: a coincidence of two or more blocks is much less likely to be random than a coincidence of two or more bytes:

>>> scores = [icoincidences(c.nblocks(16)) for c in ciphertexts]

>>> scores_and_indexes = [(s, i) for i, s in enumerate(scores)]
>>> scores_and_indexes.sort()
>>> scores_and_indexes[-1:] # higher values, less random
[(0.133333333<...>, 132)]

>>> methods['IC - Nblocks sequence'] = scores

Scores by method.

For the Nblocks method, the size of the block is of 16 bytes.

Note how the Index of Coincidence (IC) detects the non-random ciphertext in both cases but it is much clearer when the IC is computed on 16-bytes blocks.

This is because ECB encrypts to the same cipher block when the plain blocks are the same.

Other vulnerable encryption modes will not be as easily detectable however.

Broken?

Well, distinguishing a encryption from a random string is enough to considere a cipher broken, but trying to get the plaintext from it is another level.

The 132th plaintext will still be a secret, for now.